مقدمه
در زمینه علوم و مهندسی مدرن، ادغام نقشی محوری دارد. این پایه و اساس بسیاری از محاسبات است، از حل معادلات دیفرانسیل پیچیده تا محاسبه مناطق زیر منحنی. با این حال، با پیچیدهتر شدن محاسبات و فشردهتر شدن دادهها، روشهای سنتی اغلب کوتاه میآیند و زمان و منابع قابل توجهی را مصرف میکنند. Torchquad را وارد کنید، یک پلاگین پایتون که در شرف تغییر بازی است

معرفی کوتاه Numerical Integration
Numerical Integration روشی اساسی است که در ریاضیات و علوم محاسباتی برای تقریب انتگرال های معین استفاده می شود. این تکنیک زمانی به کار می رود که به دست آوردن یک راه حل تحلیلی برای یک انتگرال دشوار باشد یا زمانی که تابعی که باید یکپارچه شود فقط به عنوان نقاط داده در دسترس است. در حالی که ادغام تحلیلی راه حل های دقیقی را ارائه می دهد، ادغام عددی راه حل های تقریبی را ارائه می دهد که برای بسیاری از مسائل دنیای واقعی بیش از اندازه کافی است.
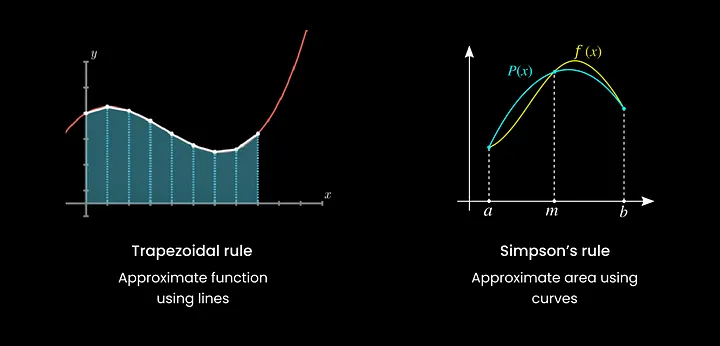
روش های مختلفی برای ادغام عددی وجود دارد
قانون ذوزنقه ای
قانون سیمپسون
ربع گوسی
روش مونت کارلو
هر روش بسته به ماهیت عملکرد ادغام شده و دقت مورد نیاز، نقاط قوت و ضعف خود را دارد. برای مثال، قانون ذوزنقهای از یک سری ذوزنقهها برای تخمین مساحت زیر منحنی استفاده میکند، در حالی که قانون سیمپسون از سهمیها استفاده میکند. از طرف دیگر، ربع گاوسی روش پیشرفته تری است که دقت بالایی را برای توابع چند جمله ای فراهم می کند.
در حالی که این روشهای یکپارچهسازی عددی سنتی مفید بودهاند، میتوانند از نظر محاسباتی گرانتر شوند هنگام برخورد با انتگرالهای با ابعاد بالا یا مجموعه دادههای بزرگ. هر نقطه داده اضافی به طور قابل توجهی زمان محاسبه را در چنین سناریوهایی افزایش می دهد و این روش ها را کمتر امکان پذیر می کند. اینجاست که روشها و ابزارهای محاسباتی جدید مانند Torchquad وارد عمل میشوند و از قدرت شتاب GPU برای انجام یکپارچهسازی عددی با سرعتهای بسیار سریعتر و با دقت بیشتر استفاده میکنند.
راهنمای نصب
ابتدا باید مطمئن شوید که PyTorch را با پشتیبانی CUDA نصب کرده اید. برای این کار می توانید این آموزش را دنبال کنید.
هنگامی که PyTorch با پشتیبانی CUDA نصب شده است، می توانید این خطوط را در کنسول خود اجرا کنید:
کوندا
conda install torchquad -c conda-forge
پایتون
pip install torchquad
پس از نصب Torchquad، می توانید با اجرای این کد در اسکریپت Jupyter Notebook/Python تست کنید که همه چیز کار می کند
import torchquad
torchquad._deployment_test()اگر با مشکل مواجه شدید، می توانید از اسناد رسمی دیدن کنید
https://github.com/esa/torchquad?source=post_page-----c5f1fd32163d--------------------------------مثال ها
اول از همه، تمام کتابخانه های لازم را وارد کنید
import numpy as np
import torch
import sympy as smp
import matplotlib.pyplot as plt
from torchquad import Simpson, MonteCarlo, set_up_backend
from scipy.integrate import quadسپس، ما باید پشتیبان و پشتیبانی GPU خود را تنظیم کنیم
# Enable GPU support if available and set the floating point precision
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(device) # This will print "cuda" if everything work correctly
set_up_backend("torch", data_type="float32")حالا اولین مشکل ماست. فرض کنید که باید این انتگرال را به صورت عددی حل کنیم

با اسکیپی، به این صورت خواهد بود:
def integrand(x):
return np.cos(x) / (1 + np.sin(x))
quad(integrand, 0, np.pi/2)
# (0.6931471805599454, 7.695479593116622e-15)در Torchquad باید از توابع PyTorch استفاده کنیم، بنابراین به شکل زیر خواهد بود
def integrand_pytorch(x):
return torch.cos(x) / (1 + torch.sin(x))
integrator = Simpson() # Initialize Simpson solver
integrator.integrate(integrand_pytorch, dim=1, N=999999,
integration_domain=[[0, np.pi/2]],
backend="torch",)
# 0.6931ما می توانیم از یکپارچه کننده های مختلف استفاده کنیم، به عنوان مثال، روش مونت کارلو
def integrand_pytorch(x):
return torch.cos(x) / (1 + torch.sin(x))
integrator = MonteCarlo() # Initialize Simpson solver
integrator.integrate(integrand_pytorch, dim=1, N=999999,
integration_domain=[[0, np.pi/2]],
backend="torch",)
# 0.6927می بینید که خطا اکنون بزرگتر است، زیرا مقدار واقعی به 0.6931 نزدیکتر است، اما این بار 0.6927 داریم.
اکنون، مشکل دوم ما – انتگرال 5 بعدی

در اینجا چیزی است که در Scipy به نظر می رسد
%%timeit
def integrand(*x):
return np.sum(np.sin(x))
nquad(integrand, [[0, 1]] * 5)[0]
# Result: 2.2984884706593016
# Time: 31.8 s ± 594 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)Torchquad
def integrand_pytorch(x):
return torch.sum(torch.sin(x), dim=1)
N = 1000000
integrator = Simpson() # Initialize Simpson solver
integrator.integrate(integrand_pytorch, dim=5, N=N, integration_domain=[[0, 1]] * 5)
# Result: 2.2985
# Time: 3.59 ms ± 113 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)شما می توانید با استفاده از انواع داده های مختلف، دقت (پارامتر N)و انتگرال گیرهای مختلف، دقت را افزایش دهید. شما می توانید تمام یکپارچه کننده های موجود را در اینجا پیدا کنید.
کارایی
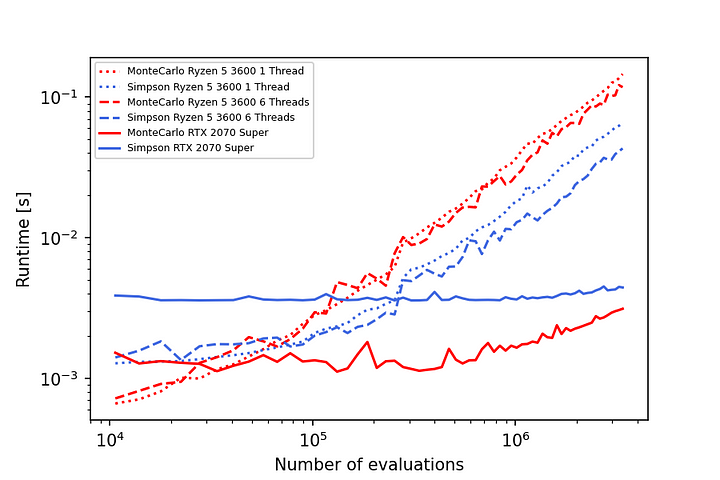
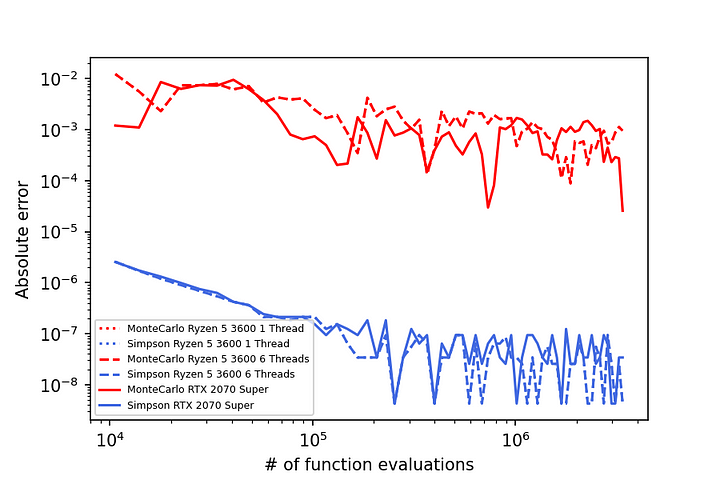
با استفاده از پردازندههای گرافیکی، Torchquad با روشهای یکپارچهسازی که موازیسازی آسان را ارائه میکنند، به خوبی مقیاس میشود. به عنوان مثال، در زیر، نتایج خطا و زمان اجرا را برای ادغام تابع f(x,y,z) = sin(x * (y+1)²) * (z+1) در رایانه رومیزی درجه یک مصرف کننده مشاهده می کنید.
نتیجه گیری
ادغام عددی در علوم ریاضی و محاسباتی ضروری است و اغلب تنها رویکرد عملی را برای حل مسائل پیچیده و دنیای واقعی ارائه می دهد. با این حال، همانطور که ما به محاسبات پیچیده تر و مجموعه داده های بزرگتر می پردازیم، روش های سنتی ممکن است کوتاهی کنند و راه حل قدرتمندتری را طلب کنند.
اینجاست که TorchQuad وارد عمل میشود و با رویکرد شتابدهنده GPU برای یکپارچهسازی عددی، انقلابی در این زمینه ایجاد میکند. با استفاده از سرعت و کارایی پردازندههای گرافیکی مدرن، راهحلی سریعتر و دقیقتر ارائه میدهد و برای طیف گستردهای از کاربران، از دانشآموزان گرفته تا محققان باتجربه، قابل دسترسی است




